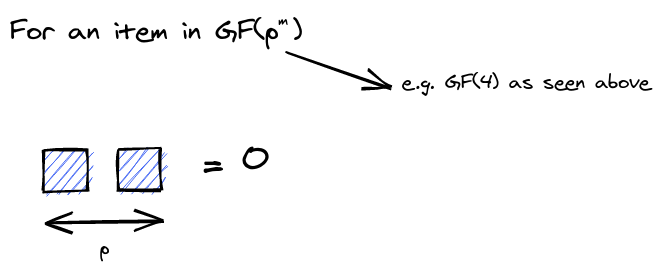
Finite Fields
CaC
A group must follow the following rules
Associativity:
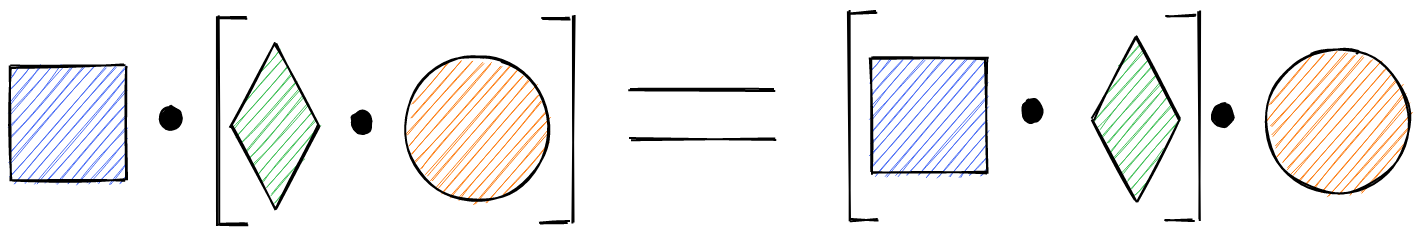
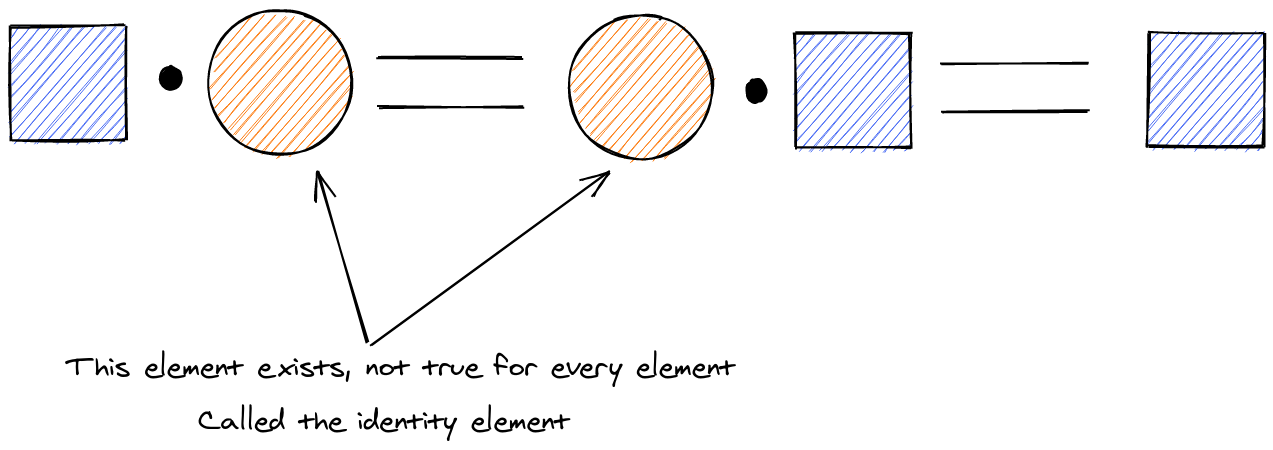
Identity element:
Inverses:
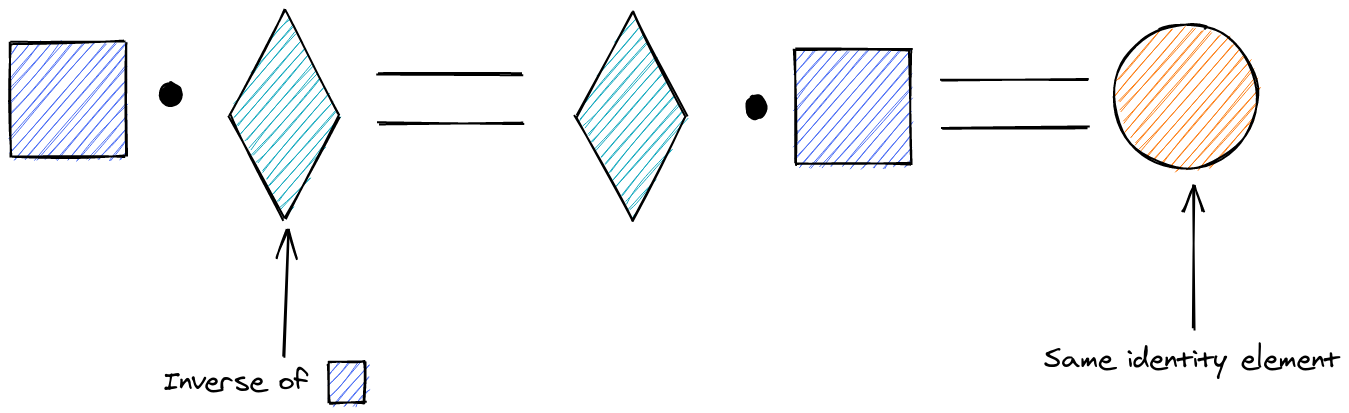
Abelian group
An abelian group is also commutative:
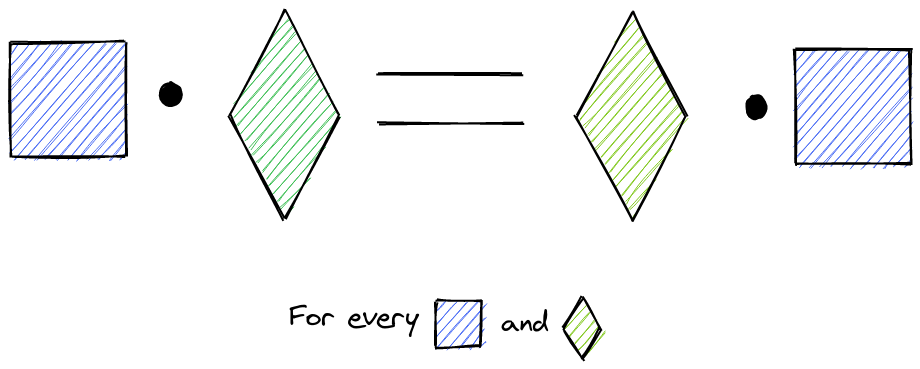
Field
A field is a 5-tuple
$$(F, +, \times, 0, 1)$$
with
$(F, +)$ being an Abelian group with identity 0
e.g. $1+0=0+1=1$
$(F*, \times)$ being an Abelian group with identity 1
e.g. $2\times 1=1\times 2 = 2$
Multiplication distributes over the addition

Galois field
Theorem
Any finite field is of order $q=p^m$, where p is a prime number and m is an integer $\geqslant 1$. All fields of a given size are the same.
These have two different notations that mean the same thing, $GF(q)$ and $\mathbb{F}_q$
Extension field
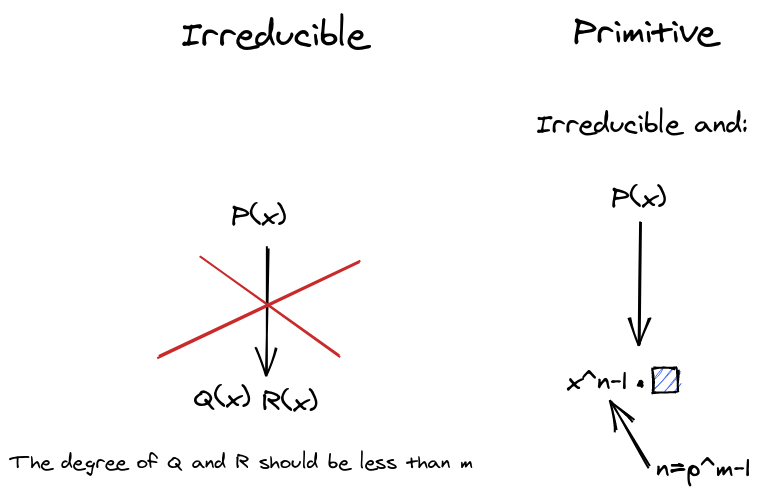
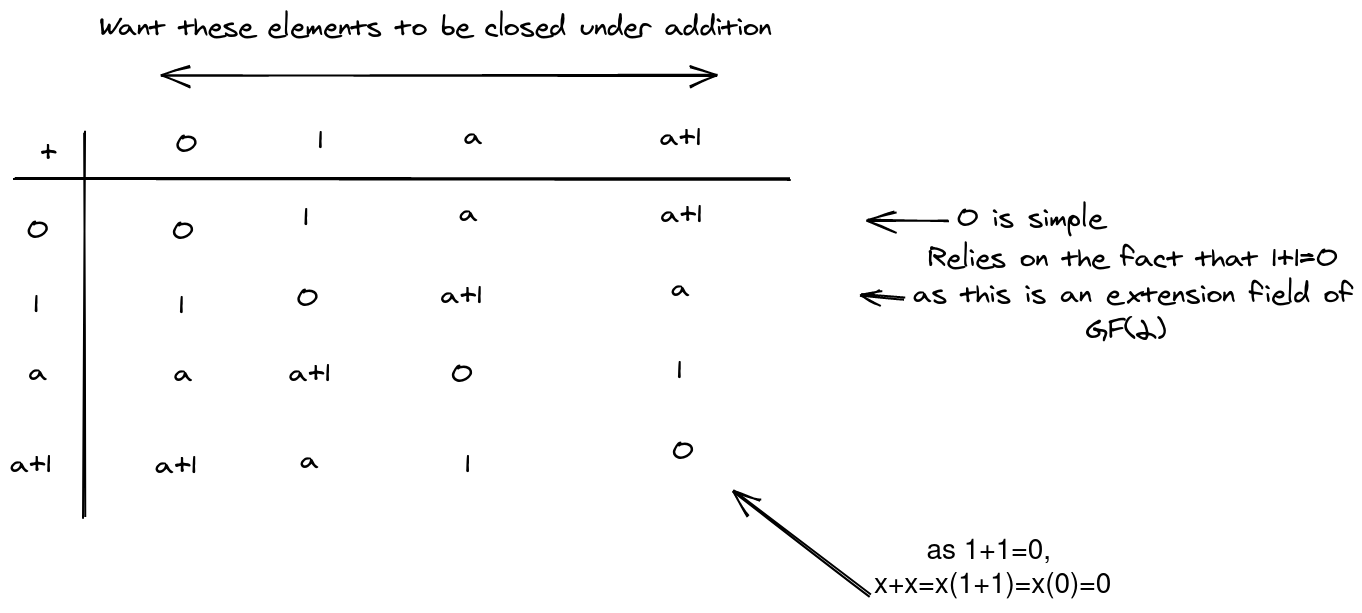
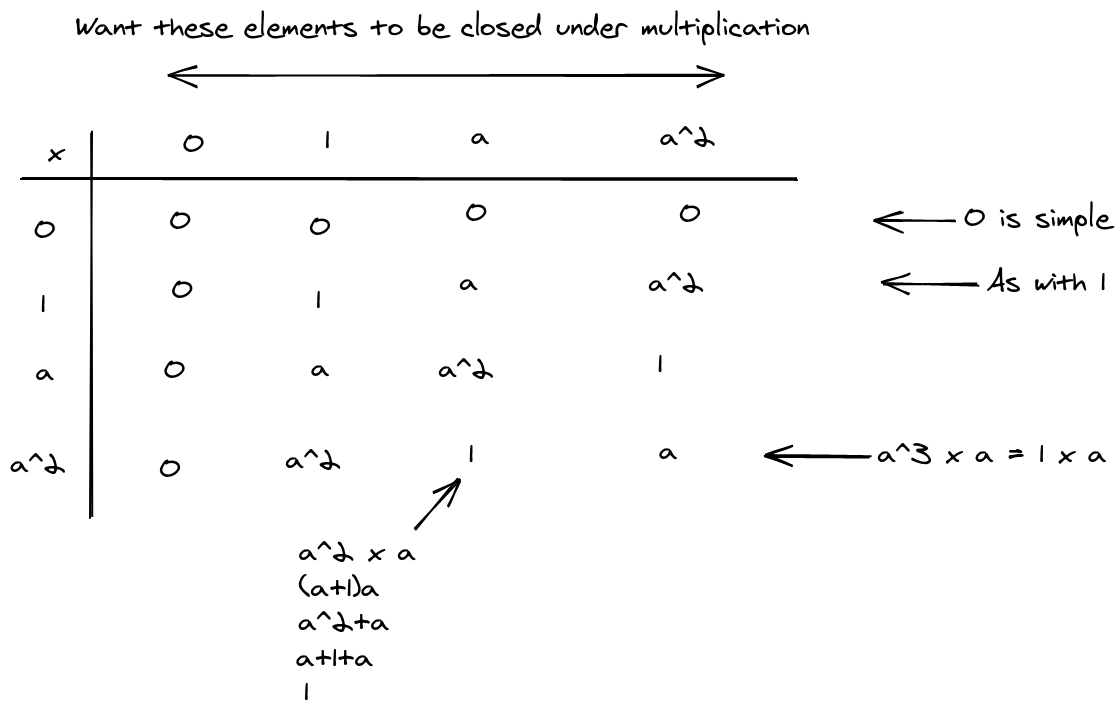
Properties
Multiplicative structure
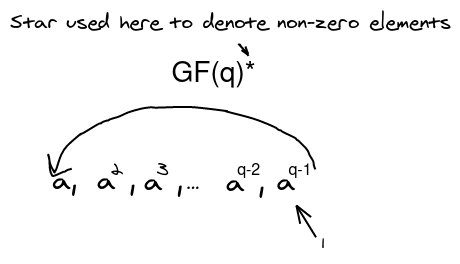
Additive structure