
## Parity Check code

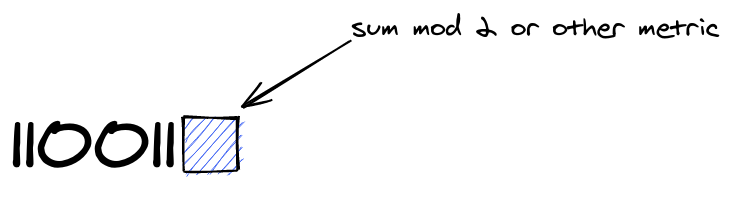
![Parity Check](/img/Uni/CaC/ECC/parity_check.png)

Can only detect **one** error and cannot correct any errors

## Repetition Code

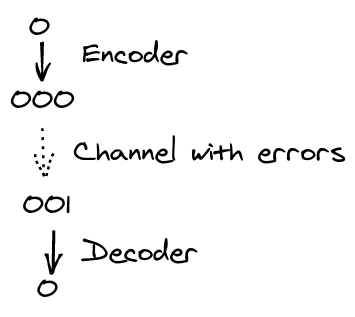
![Repetition Code](/img/Uni/CaC/ECC/repetition_code.png)

Can correct

$$
\bigg\lfloor \dfrac{n-1}{2} \bigg\rfloor
$$

errors

and can detect $n-1$ errors

## Hamming distance

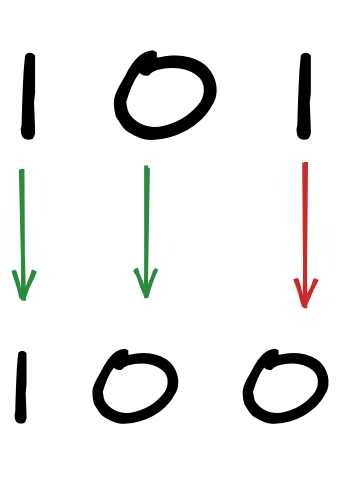
![Hamming Distance](/img/Uni/CaC/ECC/hamming_distance.png)

Measures the number of differences (in this case 1)

The **Hamming weight** is the number of non zeroes (2 for top, 1 for bottom)

## Minimum distance

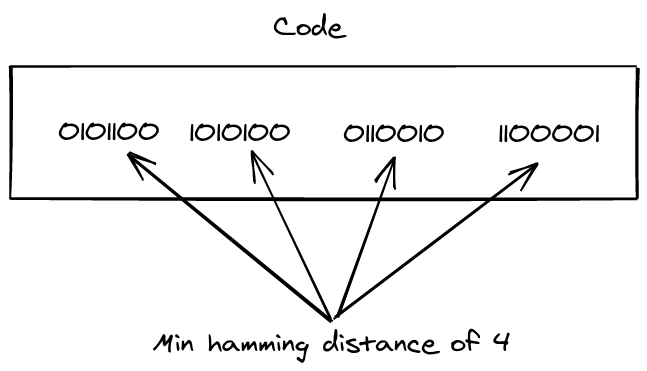
![Minimum Distance](/img/Uni/CaC/ECC/minimum_distance.png)

A code can correct t errors iff it has a minimum distance

$$
d_{min}\geqslant 2t+1
$$

So for this code it can correct 1 error (min distance of 3 would also work to correct 1 error)

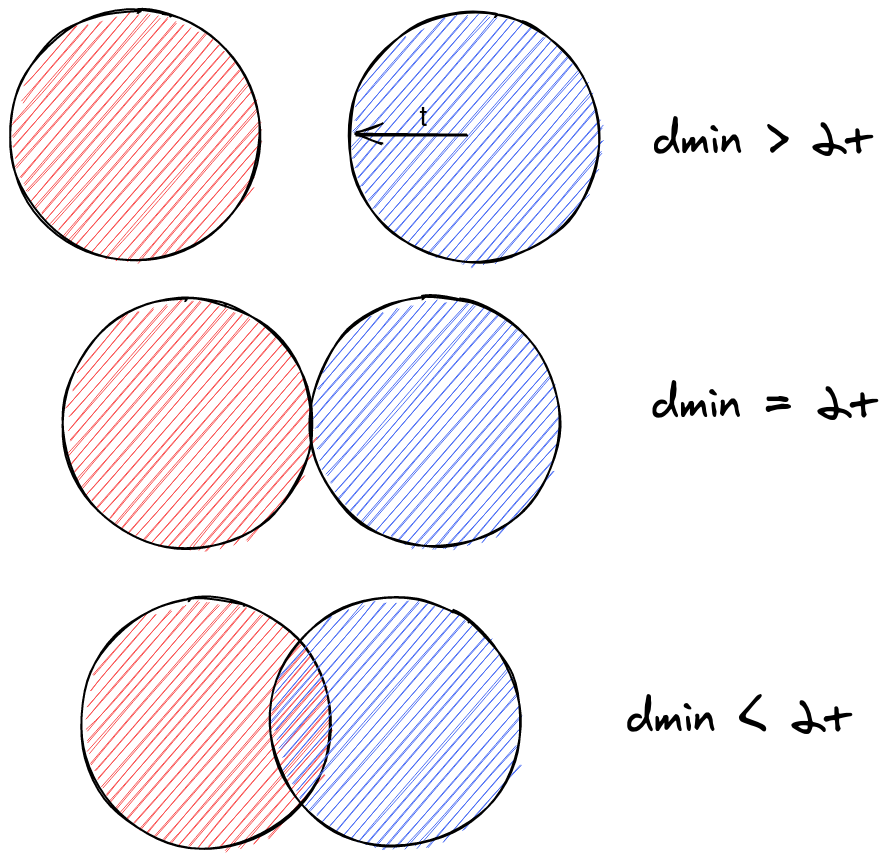
![Minimum distance proof](/img/Uni/CaC/ECC/mind_proof.png)

There needs to be overlap between the codes in order to be able to distinguish them

As the $d_{min}$ is an integer value, the formula is equivalent to $d_{min}>2t$


Error correcting codes

Architecture_and_Service.md

Compute.md

Core_Cloud_Services.md

Costs_and_Spending.md

Creating_an_account.md

Data_Storage.md

Managing_Services.md

Networking.md

Policy.md

Principles_of_cloud_computing.md

Resource_Manager.md

Security.md

AZ900

Certifications

Commands.md

GitKraken.md

Introduction.md

Fork_and_PR.md

GitHub

Boilerplate.md

Links_and_Images.md

Lists.md

Tables.md

Text_Formatting.md

HTML

Code.md

Markdown

Open_Source

Information_Theory

Cuckoo_Hashing.md

Probability.md

DADS

University_Illustrations

notes